MATHEMATICAL FUNCTIONS

Did you know that functions are a fundamental concept in mathematics? Here you'll find few basic functions and some of their key properties. Follow along to level up your math knowledge!

1. Polynomial Function A polynomial function is a mathematical function of the form f(x) = a_n x^n + a_(n-1) x^(n-1) + ... + a_1 x + a_0, where a_n to a_0 are constants and x is the variable. The degree of the polynomial is n and it can have multiple roots. Eg: f(x)=2x^3-3x+1

2. Algebraic Function An algebraic function is a function that can be expressed as a combination of algebraic operations (addition,subtraction,multiplication,division) and roots of polynomials. Eg: f(x) = sqrt(x^2 - 1)

3. Rational Function A rational function is a function that can be expressed as the ratio of two polynomials. Eg: f(x) = (3x^2 + 2x - 1)/(x^3 - 4x) The denominator cannot equal zero, as this would create a vertical asymptote.

4. Exponential or Logarithmic Function Exponential functions have a variable in the exponent, such as f(x) = 2^x. Logarithmic functions are the inverse of exponential functions, such as f(x) = log2(x). Both are commonly used in modeling growth, decay, and other phenomena.

5. Absolute Value Function The absolute value function is defined as f(x) = |x|, where the output is always the distance between x and zero on the number line. Eg: f(-3) = 3 and f(4) = 4. The graph of the absolute value function is V-shaped.

6. Signum Function The signum function is defined as - sgn(x) = -1 if x < 0 sgn(x) = 0 if x = 0 and sgn(x) = 1 if x > 0. Eg: sgn(-5) = -1, sgn(0) = 0, and sgn(8) = 1.

7. Greatest Integer Function The GIF (greatest integer function), also known as the floor function, returns the largest integer less than or equal to the input. Eg: GIF(3.7) = 3 and GIF(-2.3) = -3.

8. Fractional Part Function The fractional part function, denoted by {x}, returns the decimal portion of the input x. Eg: {3.7} = 0.7 and {-2.3} = 0.7.

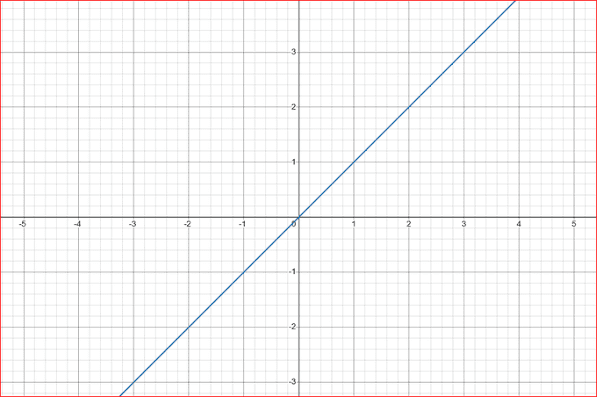
9. Identity Function The identity function is defined as f(x) = x, which means that the output is always equal to the input. Eg: f(5) = 5 and f(-2) = -2.

10. Constant Function A constant function is defined as f(x) = c, where the output is always equal to a fixed constant c. Eg: f(x) = 4 is a constant function, and the output is always 4 regardless of the input x. Constant functions have a horizontal line as their graph.

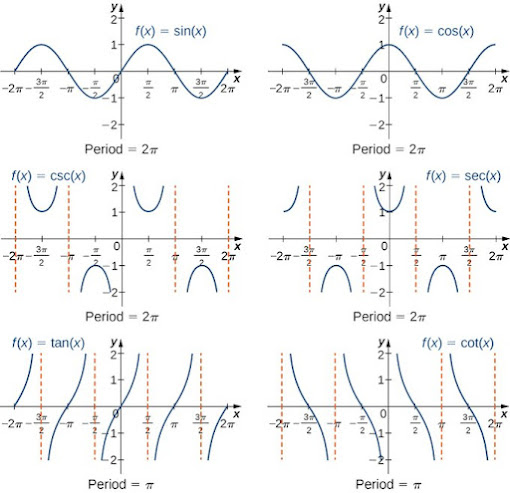
11. Trigonometric Functions Trigonometric functions are functions of an angle that relate to the ratios of the sides of a right triangle. Examples include sine (sin), cosine (cos), and tangent (tan). For example, sin(30°) = 0.5 and tan(45°) = 1

12. Inverse Trigonometric Functions Inverse trigonometric functions are functions that provide an angle given a trigonometric ratio. Examples include arcsine (sin^-1), arccosine (cos^-1), and arctangent (tan^-1). Eg: sin^-1(0.5) = 30° and tan^-1(1) = 45°.