Conics Made Simple

Are you ready to explore the fascinating world of conics?
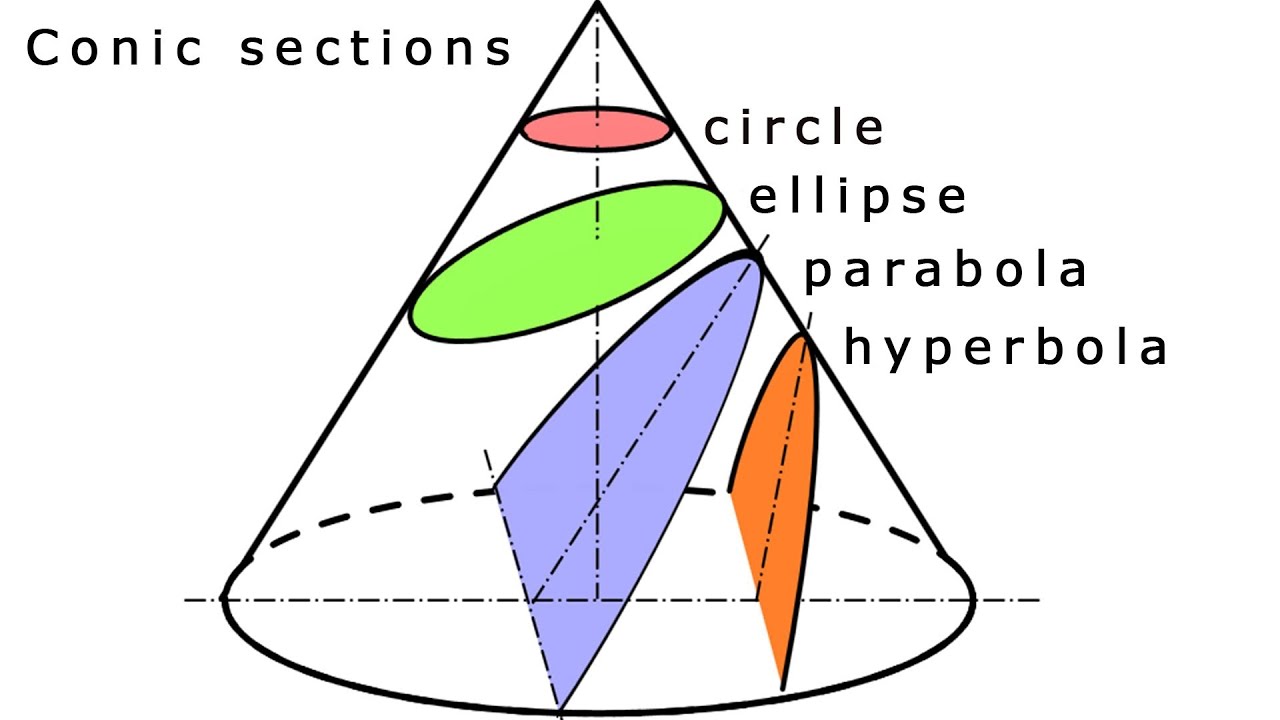
In mathematics, conics are curves formed by intersecting a cone with a plane. Let's dive in and unravel the mysteries of these geometric wonders!

1. Circle A perfect symmetrical shape, the circle is a conic with all points equidistant from the center. Its equation is (x-h)² + (y-k)² = r², where (h, k) represents the center coordinates and r is the radius.
   
2. Ellipse An elongated circle,the ellipse has two foci.The sum of the distances from any point on the ellipse to the foci is constant Its general equation is ((x-h)²/a²) + ((y-k)²/b²)=1, where (h,k) are the center coordinates,and a&b are the semi-major & semi-minor axes
   
3. Parabola A U-shaped curve with a single focus, the parabola has an axis of symmetry. Its equation depends on whether the focus is above (opening upward) or below (opening downward) the vertex. For the upward-opening parabola, it is y = a(x-h)²+k.
   
4. Hyperbola 2 branches moving away from each other It has 2 foci.The difference of the distances from any point on the hyperbola to the foci is constant Its general equation is ((x-h)²/a²)-((y-k)²/b²)=1 (h,k) represent the center,and a&b are the semimajor & minor axes.
   

Understanding conics can unlock a world of mathematical possibilities From analyzing satellite orbits to designing roller coaster,their versatility knows no bounds! Next time you spot a conic,marvel at its elegance&appreciate the mathematical brilliance behind it.

That wraps up our journey into the realm of conics! I hope this thread helped demystify these captivating curves. Remember, mathematics is not just about numbers but also about the beauty and patterns that shape our world. Stay curious and keep exploring!